

The roller support is similar to a pin support but mounted on wheels. In 2-D, the reaction force of a pin can be broken down into two component forces parallel to the x and y axes.
Thus, the pin support exerts forces in any direction, but it cannot exert a moment about the axis of the pin. The pin prevents translation but permits rotation. With a pin support, a bracket and an object are connected by means of a smooth pin passing through the object and connected to the bracket. They are the pin support, the roller support, and the fixed support. To better understand the relationship between support conventions and support reactions, detailed explanation of three of the more commonly used support conventions are presented below. The table to the left shows common 2-D support conventions.

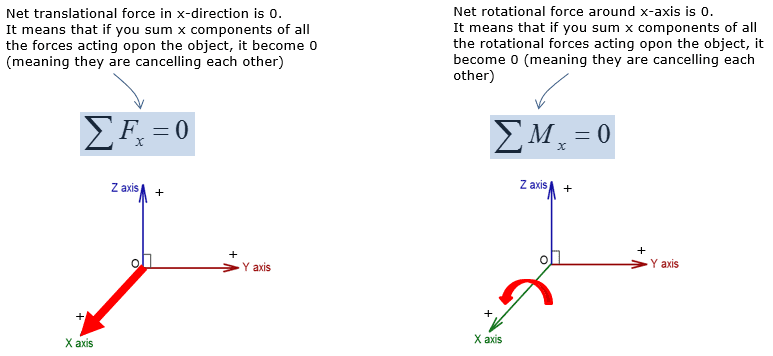
Supports can be broken down into two categories: 2-D supports and 3-D supports. Then the support exerts a couple, or moment, in the direction of the rotation. In general, if a support prevents translation in a given direction, then the support exerts a force in that direction. These forces and moments are reacting to external loads that are applied to the rigid body. The forces and moments exerted on a rigid body by its supports are called reactions. An actual support may be a close approximation of a model. Supports that are commonly found in statics can be represented by stylized models called support conventions. eCourses.ou.edu will close.īefore the equilibrium of rigid bodies can be investigated, the supports that hold them in place, or hold them to other objects, must be first analyzed.
Statics rigid body equilibrium 3d how to#
This is not to say that it is impossible to find all reaction force on an over-constrained system, just that you will not learn how to find them in this course.New eBook website Please update bookmarks. In terms of force and moment equations, there are more unknowns than than equilibrium equations so they can’t all be determined. On the other hand, if there are more reaction components than degrees of freedom, the system is both over-constrainedand indeterminate. This means that we can determine no more than three unknown reaction components in two-dimensional systems and no more than six in three-dimensional systems.Īn indeterminate system with fewer reaction components than degrees of freedom is under-constrained and therefore unstable. Each equilibrium equation derives from a degree of freedom of the system, so there may be no more unknowns than degrees of freedom. In order for a system to be determinate the number of unknown force and moment reaction components must be less than or equal to the number of independent equations of equilibrium available.


 0 kommentar(er)
0 kommentar(er)
